|
About polyhedra
|
Polyhedra hold a special place in my heart. Somehow they appeal to me at many different levels.
Deep inside, I'm a mathematician, and polyhedra bridge the mathematical world and the real world. They're not the only  mathematical objects that have a close relationship with the real world, since several kinds of fractals bear undeniable similarities with natural objects. However, while fractals are typically used to build mathematical models of real-world objects, I see that relationship working in the other direction for polyhedra, i.e. where physical models can be built from mathematical objects.
Polyhedra have been studied throughout history, and in many circumstances in the domain of polyhedra the line between mathematics and art has been a fuzzy one: without the help of computers to render complex shapes, many mathematics papers about polyhedra are works of art of their own. Leonardo da Vinci's illustrations 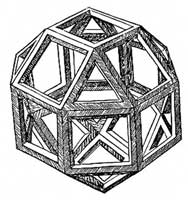 of Luca Pacioli's De Devina Proportione ("The Divine Proportion", i.e. the golden ratio) come to mind. On the German side, Albrecht Dürer and Johannes Kepler obviously can't be ignored. Closer to us, M.C. Escher has used several different polyhedra in many of his woodcuts (and some of the two-dimensional techniques he used in his two-dimensional tilings are relevant to polyhedra, since a tiling is just a flat polyhedron). Finally, George Hart is possibly the most prominent polyhedron artist those days, with a deep knowledge about the underlying mathematics of polyhedra, and a seemingly unending creativity that spans both the mathematical universe and the real one.
Polyhedra are relevant in many kinds of arts and crafts, since they can be built  from many different kinds of materials with many different techniques. They can be carved from solid materials, they can be built hollow, and the faces themselves can be cut out so that only the edges remain. They can be crafted from "raw" materials like paper, cardboard, papier mâché, foam, wood or metal. They can also be built by properly assembling other objects, in the same way that George Hart created some polyhedra-related sculptures that way from plastic utensils, CDs, toothbrushes, or custom-cut sheets of paper, acrylic, wood or metal.
 Last but not least, polyhedra are used in various kinds of toys and games. As an example, Tupperware's classic Shape-O® Toy is more or less shaped after a dodecahedron. RPG players routinely use regular and isosceles tetrahedra (D4), regular hexahedra (a.k.a. cubes) (D6), regular octahedra (D8), pentagonal trapezodra (D10), regular dodecahedra (D12), regular icosahedra (D20) and even sometimes tetrakis hexahedra (D24) and rhombic triacontahedra (D30) as their dice. Finally, a variety of contruction toys can be used to build polyhedra, starting with the limited capabilities (at least as far as polyhedra go) of LEGO and K'NEX all the way to the extreme flexibilty of Zome, with some other kinds along the way, like Magnetix, Polymorf, Jovo, or the discontinued Googolplex that each have their strengths and weaknesses.
|
|
Home page
|
Related articles
|
Posted on Apr 21 2007
|